- Criba de EratóstenesEste procedimiento permite determinar todos los números primos hasta un número determinado.
Se realiza recorriendo la tabla con los números de números utilizando el siguiente algoritmo:- Partiendo del número 2, lo resaltamos como número primo y luego tachamos todos los demás números pares múltiplos de 2.
- Continuamos con el número 3, lo resaltamos como número primo y después tachamos los demás números múltiplos de 3.
- El siguiente número primo de la tabla es el 5, lo resaltamos como número primo y luego tachamos todos los demás números múltiplos de 5.
- Hipótesis de Riemann
Esta hipótesis es conocida como uno de los 7 problemas del milenio y está aún sin demostrar. Para quien lo consiga, el Clay Mathematical Institute, ha ofrecido un premio de 1.000.000 de dólares.
Para explicarlo, debemos tener presentes algunos conceptos básicos:- Los números complejos: si nos preguntamos ¿cúal es la raíz cuadrada de un número negativo?, la solución matemática sería (-1)1/2 = i (la raíz cuadrada de -1 es i).
Este tipo de números también se pueden representar en un gráfico, utilizando el eje horizontal para los número reales y el vertical con los números imaginarios. De esta forma obtenemos un plano complejo.
Los números complejos que se muestran dentro de dicho plano se pueden representar como a+bi. Los número reales serán sólo b=0. - Las funciones: son estructuras que, dependiendo del valor que le demos a la variable incógnita (x) nos devolverá un determinado valor para la función. Generalmente se representa la función con la letra f, y la variable incógnita con la letra x quedando la estructura de la función como f (x) = x 2.
Podemos obtener, entonces, una función compleja sustituyendo la variable incógnita x por i, quedando la función f (i) = -1 y de esta forma conseguir cualquier número complejo como resultado. - La función de Riemann: se la representa con la letra griega zeta (ζ) e indica que "para cualquier número complejo a+bi la función dará como resultado otro número complejo c+di", siendo ζ(a+bi)=c+di
- Los números complejos: si nos preguntamos ¿cúal es la raíz cuadrada de un número negativo?, la solución matemática sería (-1)1/2 = i (la raíz cuadrada de -1 es i).
1x05 - Números primos sospechosos
1x04 - Fallo de estructura
- Memoria eidética
"La memoria eidética, o fotográfica, es la capacidad de recordar cosas oídas y vistas con un nivel de detalle casi perfecto. Se trata de un tipo de memoria de caracter casi sensorial, cuyo tiempo de permanencia ronda los 20 milisegundos. Precede a la memoria a corto plazo.
En filosofía, eidética refiere al conocimiento intuitivo de la esencia (del griego eidés). La diferente posibilidad de conocimiento de el fenómeno (apariencia) y el númeno (la cosa en sí) es una discusión que viene desde Kant, al menos. Se puede añadir que la distinción entre el conocimiento de la cosa en si y el conocimiento de nuestra percepción de la cosa es el tema fundamental de la "Alegoría de la Caverna" del filósofo griego clásico Platón. Para la solución de la corriente de la fenomenología, a partir de Edmund Husserl, el concepto de eidética es central.
En psicología, las personas con hipertrofia de la memoria eidética pueden recordar cualquier cosa que hayan visto u oído, incluso aunque lo hayan percibido una sola vez y de forma fugaz, en general los recuerdos son menos claros y detallados que las percepciones, pero a veces una imagen memorizada es completa en cada detalle. Este fenómeno se da con frecuencia en los niños, quienes a veces son capaces de reconstruir una imagen tan completa que pueden llegar a deletrear una página entera escrita en un idioma desconocido que apenas han visto durante unos momentos. Los que tienen memoria eidética son capaces de rebobinar los datos de sus percepciones visuales mediante su memoria eidética y proyectarlos sobre la pantalla de un lienzo." (Fuente: Wikipedia)

- Navaja de OckhamTambién llamado Principio de economía o Principio de parsiomonia. Se refiere a un tipo de razonamiento basado en el reduccionismo metodológico y cuyo postulado es: "Entia non sunt multiplicanda praeter necessitatem" o "Las cosas esenciales no se deben multiplicar sin necesidad".
Este postulado fue formulado por Guillermo de Ockham, un fraile franciscano y filósofo inglés.
1x03 - Vectores
- Teoría de gráficosEsta es una rama de las matemáticas, donde los problemas planteados y sus soluciones se presentan utilizando gráficos.
Dentro de éstos, se definen una serie de puntos (también llamados vértices) que se unen con líneas (llamadas aristas).
Utilizando esta teoría, podemos estudiar desde problemas muy abstractos hasta problemas reales, tal como sistemas de rutas, redes de comunicación, distribución de mercancías, etc.
El origen de esta teoría, como una rama de las matemáticas, está en los trabajos del matemático Leonhard Euler (Suiza, 1707-1783), quien llegó a resolver el "problema de los puentes de Koenigsberg".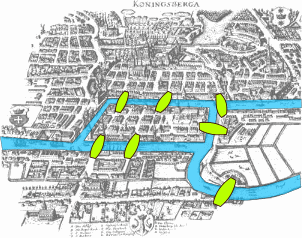
Enunciado:
"Dos islas en el río Pregel que cruza Königsberg se unen entre ellas y con la tierra firme mediante siete puentes. ¿Es posible dar un paseo empezando por una cualquiera de las cuatro pares de tierra firme, cruzando cada puente una sola vez y volviendo al punto de partida?" (Fuente: Wikipedia)
Euler demostró que no es posible dado que el número de aristas que inciden en cada vértice no es par.
1x02 - El principio de Incertidumbre
- Enunciado:
"Es imposible determinar exactamente la posición y el momento (y por tanto, la velocidad) de un sistema físico al mismo tiempo".
Otra forma de decirlo sería que, no podemos conocer los valores de las dos variables (posición y momento lineal) más allá de cierto grado de certidumbre. Si pudiésemos determinar la posición fija de una partícula, no nos sería posible conocer su velocidad, y viceversa.
De esto, a nivel microscópico, se puede deducir que: "la acción del observador altera el sistema observado".
El principio de Incertidumbre, también llamado principio de indeterminación, fue formulado por Werner Karl Heisenberg en 1927, y es uno de los principios más importantes en el campo de la física cuántica.
1x01 - Piloto
- Teoría de la supergravedad en la dimensión once"La supergravedad es una teoría propuesta para intentar unificar las dos teorías físicas que describen el universo: la mecánica cuántica y la relatividad general. Para ser coherente, la supergravedad requiere la existencia de 11 dimensiones, la mayoría de las cuales son invisibles por estar enrolladas o compactadas. Además incorpora la supersimetría.
A finales de los años 70 la supergravedad parecía una buena candidata a teoría del todo, pero partir de los 90, perdió popularidad frente a la teoría de supercuerdas, que también incorpora la supersimetría y las dimensiones extras compactas." (Fuente Wikipedia)

- Évariste Galois
Évariste Galois (25 de octubre de 1811 - 31 de mayo de 1832) fue un matemático francés nacido en Bourg-la-Reine. Mientras aún era un adolescente, fue capaz de determinar la condición necesaria y suficiente para que un polinomio sea resuelto por radicales, dando una solución a un problema que había permanecido irresoluble durante muchos años. Su trabajo ofreció las bases fundamentales para la teoría que lleva su nombre, una rama principal del álgebra abstracta. Fue el primero en utilizar el término "grupo" en un contexto matemático. - Teoría de la probabilidad
Cuando realizamos un experimento de forma aleatoria durante cierto tiempo, tarde o temprano, los resultados obtenidos tienden a presentarse de forma similar una determinada cantidad de veces.
Cuantificando el resultado del experimento aleatorio, la medida numérica asignada a la posibilidad de que ocurra un determinado suceso, se le llamará "probabilidad del suceso".
La probabilidad es una medida de la escala 0-1, de modo que si un suceso lo damos por imposible, le asignaremos el valor 0; si es seguro de que pase un determinado suceso le asignaremos el valor 1. Los demás sucesos tendrán la probabilidad de ser, y cuya medida estará entre 0 y 1.
"La teoría de la probabilidad es la teoría matemática que modela los fenómenos aleatorios. Estos deben contraponerse a los fenómenos determinísticos, en los cuales el resultado de un experimento, realizado bajo condiciones determinadas, produce un resultado único o previsible: por ejemplo, el agua calentada a 100 grados centígrados, a presión normal, se transforma en vapor. Un fenómeno aleatorio es aquel que, a pesar de realizarse el experimento bajo las mismas condiciones determinadas, tiene como resultados posibles un conjunto de alternativas, como el lanzamiento de un dado o de una moneda.Los procesos reales que se modelizan como procesos aleatorios pueden no serlo realmente; cómo tirar una moneda o un dado no son procesos aleatorios en sentido estricto, ya que no se reproducen exactamente las mismas condiciones iniciales que lo determinan, sino sólo unas pocas. En los procesos reales que se modelizan mediante distribuciones de probabilidad corresponden a modelos complejos donde no se conocen a priori todos los parámetros que intervienen; ésta es una de las razones por las cuales la estadística, que busca determinar estos parámetros, no se reduce inmediatamente a la teoría de la probabilidad en sí.
En 1933, el matemático soviético Andréi Kolmogórov propuso un sistema de axiomas para la teoría de la probabilidad, basado en la teoría de conjuntos y en la teoría de la medida, desarrollada pocos años antes por Lebesgue, Borel y Frechet entre otros.
Esta aproximación axiomática que generaliza el marco clásico de la probabilidad, la cual obedece a la regla de cálculo de casos favorables sobre casos posibles, permitió la rigorización de muchos argumentos ya utilizados, así como el estudio de problemas fuera de los marcos clásicos. Actualmente, la teoría de la probabilidad encuentra aplicación en las más variadas ramas del conocimiento, como puede ser la física (donde corresponde mencionar el desarrollo de las difusiones y el movimiento Browniano), o las finanzas (donde destaca el modelo de Black y Scholes para la valuación de acciones)." (Fuente Wikipedia)
